
这个系列写给对数学感兴趣的初学者——无论是准备报考数学系的高中生,准大一新生,在寻找方向的低年级本科生,还是想自学的数学爱好者。我希望从个人经验出发,大致梳理数学专业科技树的全貌,并且介绍一些趁手的学习工具。本篇整合一些可能有用的互联网资源(也希望抛砖收获评论区的宝玉~)
免责声明: 以下完全是一个纯数研究生的一家之言。首先我不针对任何考试(想考研就狠刷数分高代,想考丘赛就……刷真题?反正我也没考过hhh);其次,对于大学生们——你们的老师肯定比我更专业;然后,对于应数统计和转码跑路——去问别人(然后带我一个 +ω-)
绝大部分数学资源都以英语的形式存在于互联网上,获取的主要障碍只在于语言和上网工具。考虑到现代数学的教材和论文基本上都是以英语写作,学会用英语阅读甚至思考数学将是每个初学者必须面对的任务。好在数学用英语有着高度结构化和模板化的表达方式,很快就能习惯。对那些还不太习惯英语的初学者,我个人的建议是,在早期可以同时参考中文和英文教材,对照学习词汇和句法;现在翻译软件和 AI 高度发达,借助 GPT4o 或者 DeepL / Google 翻译都可以大大方便我们学习英文教材。此外,为了练习英语输出能力,也可以刻意训练使用英文做题或者写笔记。

如何规划数学学习路线?这是知乎的日经问题了:
无论是数学专业还是数学爱好者,在面对庞大的现代数学大厦面前难免踌躇。现代数学到底学些什么?在投入人生中最宝贵的几年时间之前,这就是第一个需要解答的问题。但这个问题没有标准答案,而是取决于更基本的问题——我为什么喜欢数学?我喜欢数学的什么?对数学的需求和动机将会决定你的学习内容。
无论如何,如果你的目标是在 2~3 年内全面了解某个纯数学领域的基础,达到准研究生的水平的话,希望这里的资源会对你有所帮助。
一切数学领域的共同基础是数学分析和线性代数,这样说恐怕无人会反对。一个 Bachelor in Mathematics 不一定学过某门专业课,但是一定精通数分线代。如何学习数分线代的教程在知乎上汗牛充栋。暂且让我们继续前进——
在经历 1~1.5 年的共通线学习后,此后想要继续走纯数学方向,有三条主线:分析与方程;代数与数论;几何与拓扑。想要快速了解这些方向的骨架知识,最快的方式就是参考 丘成桐大学生数学竞赛 的考纲:
Mathematical Physics(转物理)
丘赛的设计目的是对标国外名校的博士生资格考试 (qualifying exams),通过的学生即具有足够从事数学研究的知识水平。尽管可能不如丘赛全面,博资考的大纲对本科生的学习是很有指导意义的:
由于不同数学方向之间联系非常紧密,完全专精一个方向而不管其它方向是不可能的。一般来说,能在两个方向上通关丘赛考纲,已经属于特别优秀的本科毕业生了。
有了大方向之后就可以开始规划具体的学习路线图。对于这一点,很多高校的网站都提供课程目录及顺序:
国内高校的公开信息,比如北京大学的 培养方案 和 常设课程;清华求真的 培养方案;其他一些都可以在这个问题的答案里面找到:
中文资料中参考价值最高的可能是这份由中科大学生制作的 USTC基础数学修课指南,包含了一般学习建议和各个课程介绍。
MIT 的 Math Major Roadmaps.
Cambridge 的 Undergraduate Mathematics: Course Information,这里面包括从大一到大三每年详细的课程内容大纲,而每门课的非官方的讲义可以在这里找到:Tripos-specific resources;作业题在这里:DPMMS example sheets.
**强力推荐 *Oxford 数学系* 的网站:这里有从大一到大四每一门课程的大纲,讲义,习题,全部免费公开(! ω !)** 点开 Course Synopses 可以看到分年级的课程大纲集成 pdf;点开 Course planner 可以互动地探索从大二到大四每门课之间的相互依赖关系。据我所知,如此便利公开的共享资源或许独此一家吧。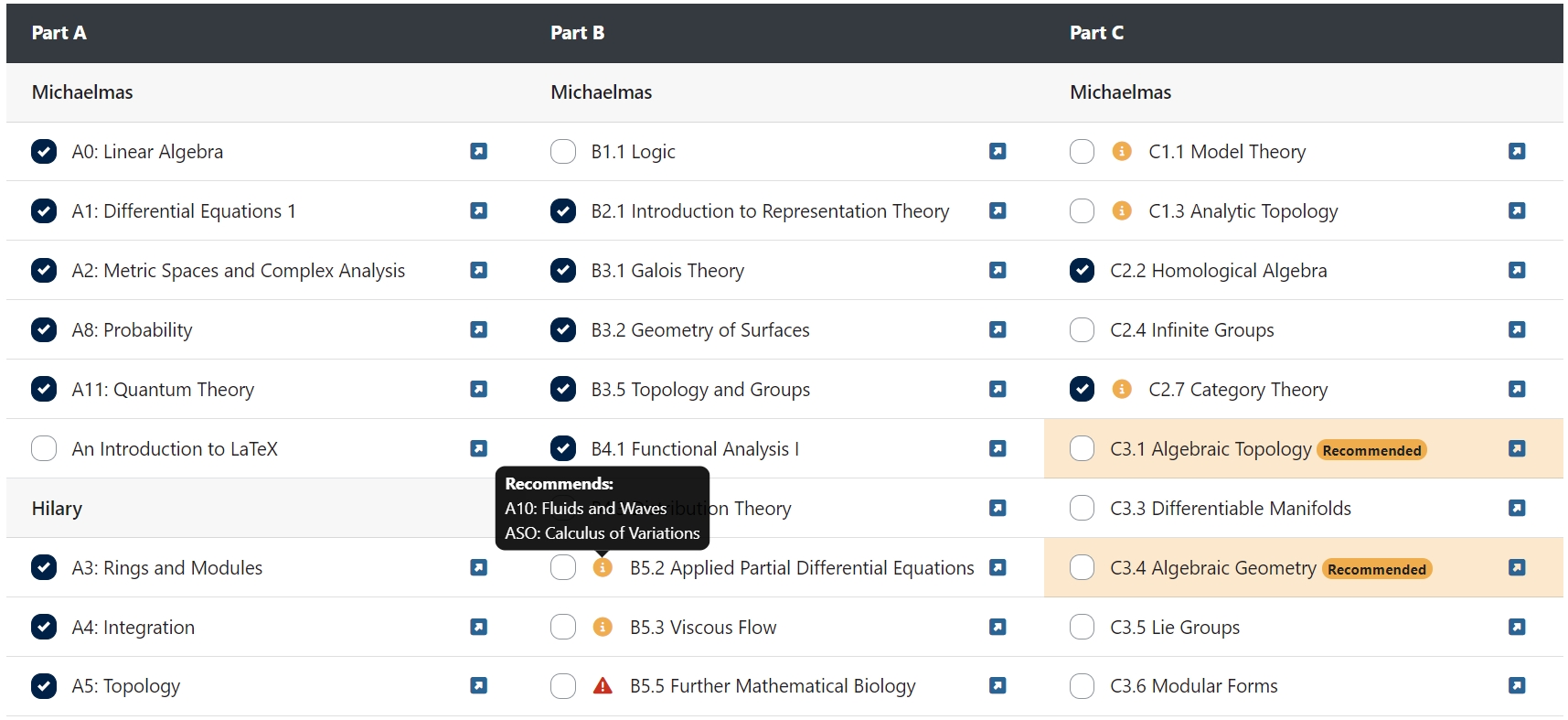
直接在知乎问!在简体中文的数理信息丰富性和专业度上,还没有平台能替代知乎。
英文的数学问答论坛就是 Math StackExchange 和 MathOverflow。前者主要是具体数学习题的答疑,后者则是讨论研究性问题以及一般问题。注意这几个网站对提问的方法有着比知乎更严格的要求,伸手党问题一般会被直接关闭;同时好的提问会得到快速解答。
其它一些活跃的中文数学社区还有 超理论坛(其中还有其他理科的板块)。
想要快速了解一个概念名词,英文维基百科是最快的方式。除此之外,具有百科性质的网站还有:
nLab 是一个以高阶结构(无穷范畴)为骨架的数学和物理百科。
香蕉百科 是一个中文数学百科,其中也有一些数学讲义和讨论。
Stacks project 是交换代数和代数几何的百科全书。由 de Jong 发起的项目,其最初目的是覆盖所有学习代数叠 (algebraic stacks) 所必须的数学,现在已经发展成超过 7500 页的百科,很多标准的代数几何结论的证明都可以在上面找到。
Kerodon 是基于 Jacob Lurie 作品的无穷范畴百科。
你能叫得出名字的本科课,在 Bilibili 上大多都能找到优质的中文课程录像。其中优质的有丘维声的 高等代数,梁灿彬的 微分几何入门与广义相对论 等。这些课程有配套书籍,按照进度跟着学能获得几乎和在校选课相当的体验。
与此相对,YouTube 上也有很多英文课程的录像,并且录像的丰富程度随着疫情时远程学习的普及有了飞跃的发展。
视频网站的另一大特色是精致的科普视频,比如 3Blue1Brown 还有 Veritasium。比起干燥的课本,这些视频能够给入门者创造动机和兴趣。我本人在学数学之前也深受 3Blue1Brown 的系列 线性代数的本质 的惠泽。
各大高校的网站,有一定概率可以找到对应课程的讲义或者其他资源,只要 Google 搜索课名+学校名就行。这里再次强推 Oxford 数学系 的网站!
如果有学生账号,并且所在大学或机构有订阅,可以在一些出版社(比如 Cambridge University Press,Springer)网站上登录后直接免费下载。
一些比较新的书,可以搜索作者的个人网站,有概率存在免费公开的版本可以直接下载。
大部分英文教材的 pdf 版都可以在 z-library 或者 Library Genesis 上找到。
如果对纸质书有特殊喜好,但是未在国内有引进出版的,可以把 pdf 在淘宝店打印装订出来,价格一般不超过小几十块钱。
数学领域几乎所有的论文在发表前都会以预印本的形式在 arXiv 上公开。如果对某个方向特别感兴趣,可以使用 arXiv 的订阅功能,它会每天发送当日在该领域的新增文章,订阅方式详见 Subscribe to daily listing emails。
想要了解某个领域内的会议汇总情况并不容易,一般靠的是口耳相传。仅就个人了解的代数几何内:
Ravi Vakil 有一个网站汇总了国外的代数几何会议情况:Upcoming conferences in algebraic geometry
据我所知还没有人汇总国内代数几何会议信息,如果有知道的欢迎汇总~
邮件订阅 COW 或者其它 mailing lists,会收到关于会议的信息,同时也有 PhD / postdoc / 教职的招聘信息,请注意这些列表是偏向于欧洲的。
请见谅这些网站的选择受到我个人兴趣的影响,因此相对偏向于代数和几何这边。首先是一些笔记狂魔:
Dexter Chua:一位剑桥本硕,哈佛博士的大神。他的网站有大量本科剑桥数学课的 LaTeX 笔记,超过 4000 页。
Gilles Castel:另一位 LaTeX 笔记大神,他著名的博文 How I'm able to take notes in mathematics lectures using LaTeX and Vim 以及其后续有非常高的参考价值。
Florian Bouyer:这位是华威的本硕博。他也写了大量数学课程笔记,从本科到研究生级别的都有,偏向代数方向。
请允许我塞进来一些理论物理私货,虽然可能不适合出现在这个数学文章当中,但是如果粗暴地认为理论物理是数学的一部分也未尝不可(bushi)。
David Tong:物理系同学中无人不晓的佟大为教授。Tong 的网站上有包罗万象的物理课程讲义,从四大力学到弦论,且平均质量极高,非常适合自学或者考前速成的时候参考。
The Theoretical Minimum:这个网站有 Leonard Susskind 讲授的各门理论物理课程的录像。所谓的 Theoretical Minimum 最初指的是大名鼎鼎的朗道势垒,意指一个合格的理论物理学生所需掌握的最少知识。
下面是一些有价值的数学家网页:
陶哲轩:陶哲轩写了大量博客,其中有很多关于数学事业和写作的建议。作为最知名的数学科普作家,他的文字对任何人都值得一读。
Mura Yakerson:Yakerson 是牛津的副教授,她运营的 YouTube 频道 Math-Life Balance 中采访了大量处于生涯活跃期的数学家,对于志在数学研究的人很有参考价值。
李文威:李文威教授火出圈的契机可能是他的两卷“高观点”写作的《代数学方法》。除此之外,他的网站上还有很多书和讲义,其中即将完工的《代数学讲义》有望成为代数学入门课程的新标杆。最可贵的是,他的代数学方法是一本完全开源的中文书,其中甚至附有书籍的 LaTeX 模板;他对排版的每个细节都很严谨,因此对于想要使用 LaTeX 进行中文写作的同学来说,这无疑是最好的参考。
梁永祺 教学与研究生指导:梁教授的网页上有很多文章,包括他自己求学代数几何时的经历,以及给学生的建议等。学代数几何前读一读很有价值。
J.S.Milne:Milne 教授的网站上也有非常多的讲义,偏向于代数和数论方向。其中比较知名的大概是他写的 Abelian Varieties 和 Étale Cohomology。
Pieter Belmans:Stacks project 和 Kerodon 的网页维护者,他还开发了很多代数几何分类相关的网站,比如 Fanography 记录了 Fano 三维簇的分类和数值不变量。
Ravi Vakil:Vakil 教授最有名的就是他还尚未出版的巨著 The Rising Sea: Foundation of Algebraic Geometry,大有超越 Hartshorne GTM 52 成为新世纪代数几何必读书目之势。他的网页上也有很多实用的建议,比如如何从数学讲座中学到东西:The "Three Things" Exercise for getting things out of talks,以及他本人对想读 Ph.D. 的学生的要求和建议:For potential Ph.D. students。
Graduate Students' Guide to Generals:这个网站搜罗了 Princeton 博士生数学口试过程的自我记录,其中不乏一些成名已久的数学家,比如许晨阳,陶哲轩,恽之玮等。从这里一窥大佬们学生时代的学习痕迹也是饶有趣味。

作者授权,转载自“知乎”的文章:https://zhuanlan.zhihu.com/p/709525527